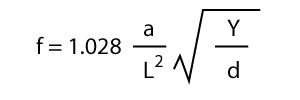So Sebastian Hurtado of Guatemala was, it seems, the first to make a fully chromatic marimba (1890s). We had to wait until the 1920s before the next essential feature of the modern marimba was introduced, namely harmonic tuning .... which is what, exactly?
Explanation, and more, follows below the fold. (This is quite a long post, but there are many illustrations to make it even more confusing).
Most people are aware that a piano string doesn't only give the note it's nominally tuned to but a whole series of higher notes (overtones or partials, in the jargon). Same for the air columns in flutes or organ pipes. This is because any regular vibrating mass combines several different modes of vibration: e.g. a string will have a simple mode of vibration where the string is most active (i.e. whooshing from side to side the furthest) at its midpoint and not whooshing at all at its ends -- this mode corresponds to the lowest audible tone; then there is a whole bunch of higher modes that have two, or three, or more, most-active-points at different locations along its length. The same (pretty much) for the gas molecules in an air column. Strings and air columns produce the same pattern of overtones (approximately) which are dignified with the name the harmonic series -- which means if you tune your piano string (organ pipe, nose flute) to C you will also be producing the C an octave above, the G above that, the next C up, then an E, another G, a (rough) B flat etc etc ...
Now a string, being quite a floppy thing, can only vibrate if it is fixed at both ends, which forces it to have points of least vibration (nodes) at its endpoints; similarly a vibrating air column is for practical purposes "fixed" at the points where it meets the rest of the atmosphere, which is a large unwieldy object and can't be made to conform to the pattern inside your pipe (apart from conveyng the tone to our ears).
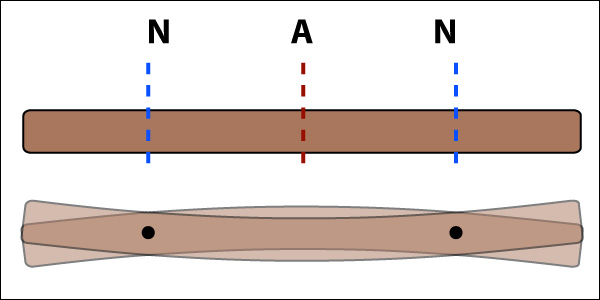
A marimba bar (xylophone bar, tubular bell ...) is different, because it is actually free to vibrate at its ends, what is technically called a free bar. Or in fact, and this sounds even more lipsmacking, a free free bar, (i.e. both ends free to vibrate, as opposed to only one as in a kalimba tongue). So when you set it vibrating (e.g. by hitting it with a stick, perhaps, while fortuitously gripping it at a node), the simplest mode of vibration will have a most-active-part -- an antinode -- in the middle, but a lot of movement at each end as well.
A cartoon of a vibrating marimba bar -- first (fundamental) mode of vibration. Someone has drilled holes for the cord right at the nodal points; smart. NB It doesn't actually move this much, obviously.
Skipping the hard sums, the upshot is that whereas a string has a series of overtones that relate to its fundamental tone by simple integers, a bar is much crankier. If the fundamental tone of a string has x vibrations per second, then the second mode has 2x vibes per sec, the third mode 3x, and so on until you run out of fingers (you understand we're talking about an ideal string here ... the real strings we have to make do with in the real world don't actually manage this kind of mathematical perfection, but they get close enough). However with a free free bar, the second mode of vibration is 2.756 times the fundamental, the third mode 5.404 times. So if your fundamental tone is C3, your first overtone will be F4 plus 55 cents or so; and your next overtone will be F5 plus about 21 cents.
Of course this is perfectly natural -- after all nice resonant sticks are probably commoner in nature than strings fixed at both ends; but it doesn't conform to human musical preferences as well as simple ratios do, it seems. So when you make a simple instrument with a bunch of free bars, there will be clouds of non-harmonic overtones accompanying all the notes. With wooden bar instruments, particularly high-pitched ones like xylophones, this hardly matters, as the overtones are very weak and barely sustain at all. However the overtones on metal bars can ring on and on in a most persistent and annoying fashion, as Herman Winterhoff proved with his Leedy Vibratone Bells, and low-pitched wooden bars (i.e. the longer ones) can also have remarkably prominent overtones.
Hmmm. How long does a bar have to be before you need to worry about overtones? Maybe not that long, because somewhere between the stone age and 1918 people had worked out that is possible (in fact easy) to make a bar longer without making it any longer.
Suppose you are wandering down the beach and decide to make a driftwood marimba from the plentiful supply of driftwood .... and in fact as you are on the Beach of Improbablility, the first eleven logs you pick up give you a perfect pentatonic scale over two octaves, say C D E G A c d e g a c'. Lucky! All these (improbable) logs are pretty much the same width, thickness and density, the only relevant factor that they differ by is length. You are pleased to discover that your low C is exactly twice as long as the C two octaves above. Here at least is a nice simple relationship. You scratch some figures in the sand to help keep it in mind -- if L (length) = f (frequency), then 2L = f/4.
Being an ambitious driftwood marimbist, you set about collecting some more logs to extend your range another two octaves in a bass-ward direction. Now things get less convenient, because your bottom C is (of course) four times as long as your top C; in fact it is nearly a metre long, and the instrument is beginning to look rather cumbersome. You worry that if you take your axe to gigs in the manner of these fellows --
-- you will be too worn out to play when you get there.
But now, more luck! The next log you collect is exactly as long and as wide as your top C, but it is only half as thick -- and astonishingly it produces the C an octave lower! So if t (thickness) = f, then t/2 = f/2. By making the lower notes successively thinner, you can also make them shorter -- you will have the pitches you want, and you will also have an eminently portable instrument (and you won't need mallets two feet long either).
The Beach of Improbability is alas not quite improbable enough to provide you with a bandsaw or a drum sanding machine, but it has plenty of abrasive rocks, so you spend some happy hours experimenting with your bars. You find that a bar does not need to be 50 per cent thinner all the way along its length to give you an octave drop. It only needs to be thinner for about the middle third. Funny! -- but mighty convenient, for these scooped-out bars (thin in the middle, fat at the ends) seem to sound rather better than bars that are thinner all the way. Also, you have ended up with a keyboard that looks rather trim, even elegant -- the bars graduate moderately from longish to shortish, and they look pretty uniform in width and thickness.
You have recapitulated some percussion prehistory.
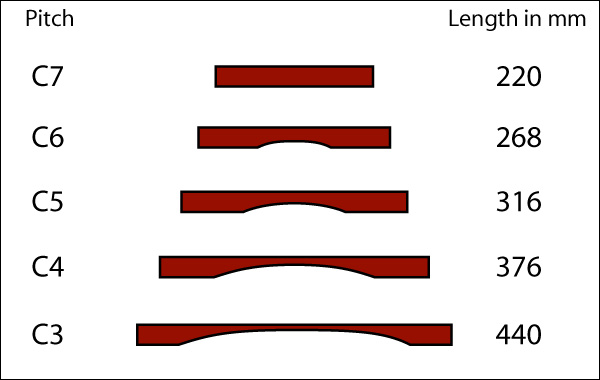
We are going to leave the beach and bring all of our C bars into the laboratory for further investigation. Here they are in profile, with their pitches and dimensions.
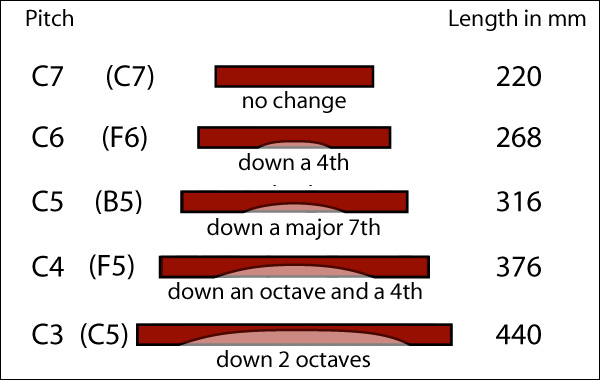
Only the C7 bar has been left untouched from its original state. All the others have been scooped out; the scoops (discovered by trial and error) get more radical as our bars get lower in pitch. Or, to be more accurate, the scoops get larger when we wish to flatten a bar by a greater distance from its original untouched state. Let us repeat our C profiles, this time adding the INITIAL pitch of each bar and the distance travelled in a flatward direction.
The precise shape of the scoops has not concerned us overmuch -- as long as we've ended up with the desired pitch we've been happy. And the exact shape doesn't seem that important. Here are several versions of a C4 bar, all produced from blanks 376mm long with an original pitch of F5.
It seems that a deep cut right in the middle of the bar is equivalent to a shallower cut spread over a wider area. It's as if the "flattening value" of removing bar material is highest at the exact mid-point, and gets less as you move away from it. And now we may as well state explicitly what you have probably guessed -- the mid-point of the bar is of course the antinode; and removing mass here makes the bar less stiff (therefore it will vibrate more slowly; for people more used to strings, think what happens when you decrease the tension in a guitar string).
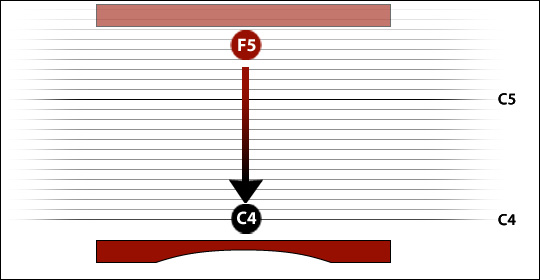
Here is our C4 bar again, but now it comes with a background of conceptual pitch space (far out!) ... the original pitch of the bar is sitting in a red bubble, vertically in line with the antinode ... superimposed on a ladder of semitones ...
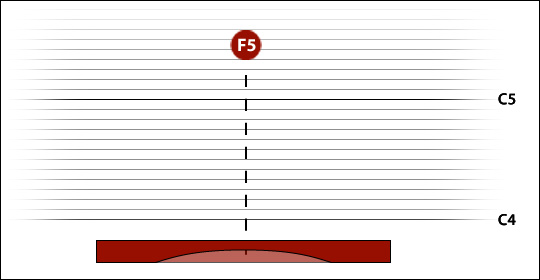
... and as we make our scoop, removing material from around the antinode, the pitch-denoting bubble descends the ladder to a new location, like so:
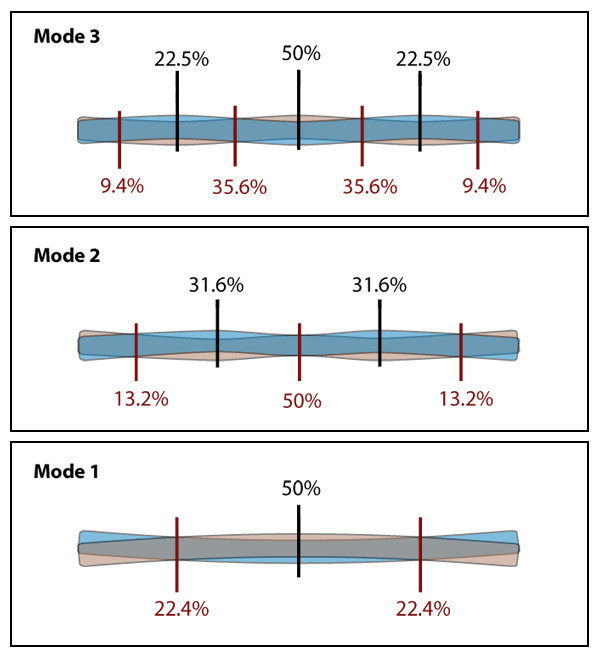
But we began this discussion by talking about multiple modes of vibration -- overtones. The higher modes are also present in our sounding bar, and they have their own locations for nodes and antinodes, as illustrated here for the first three of them:
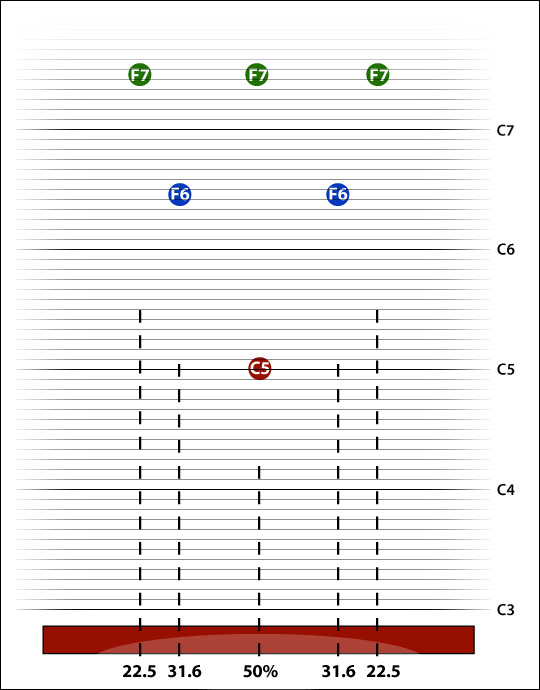
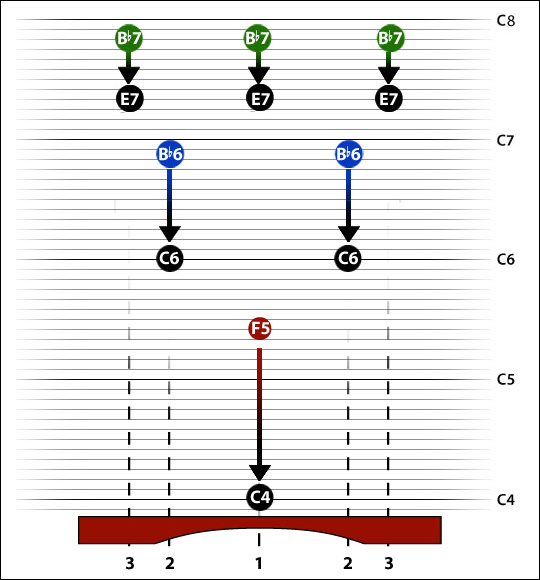
So let's represent the first three modes of vibration on our groovy pitch-space diagram. We are shifting to the C3 bar because, in case you have an actual C3 bar to hand, it will be easier to hear the overtones than with a higher-pitched bar. The pitch bubbles are located above the points on the bar that are the antinodes for that overtone (theoretical locations of the antinodes for modes two and three indicated below the bar). Remember, the initial pitch of our C3 blank is C5, so that is where our lowest bubble is located in the pitch-space. For the sake of simplicity I will ignore the exact pitch of the higher partials and just identify them by the nearest semitone.
We cut our normal scoop (the approved technical term seems to be arcuate notch), and guided by an intuition that a nice smooth elliptical shape seems most satisfying, we carry on until our fundamental tone is close enough to C3 to fool most people's ears. [NB a smooth elliptical notch is also easy to make with the kinds of tools one might have to hand -- on the beach, abrasive rocks; in an early-20th century workshop, bandsaws, drum sanders, spokeshaves, chisels ...] Having been improbably provided with a Peterson tuner, we check what has happened to the other two modes, just out of interest. And this is where they ended up:
Perhaps our intuition was being guided by our ears, as the overtones we have are now very close to the harmonic tones C5 and E6. We have overshot somewhat but it looks like it would be pretty straightforward, by modifying the exact shape of our notch, to tune this bar C3 -- C5 -- E6. And in fact it is pretty straightforward, and this is now common practice on the lower octaves of marimba keyboards for all makers, corresponding to this:--
In manufacturers' blurb this is what is called triple-tuning.
NB I have dropped the percentage locations of the antinodes and simply numbered them by the mode of vibration they belong to. When you remove mass from the middle of the bar, and change its length/pitch relationship, the locations of the nodes and antinodes also change -- they start to migrate towards the ends of the bar. There is presumably some mathematics that can tell us exactly where they should move to, but I haven't looked it up. In actual tuning practice, you can easily identify where the nodes of the fundamental mode are -- if you are holding the bar up in one hand and whacking it with a mallet held in the other hand, the bar will sound most resonant when your gripping fingers are at the nodal point. Working out roughly where the antinodes for modes 2 and 3 are is then not difficult.
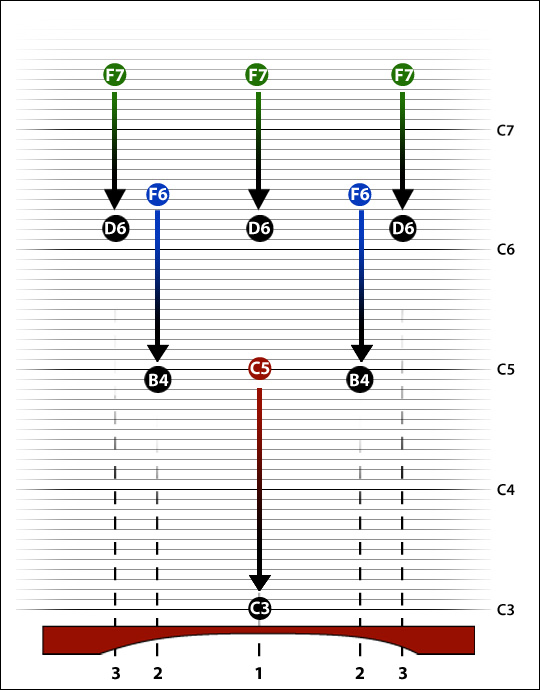
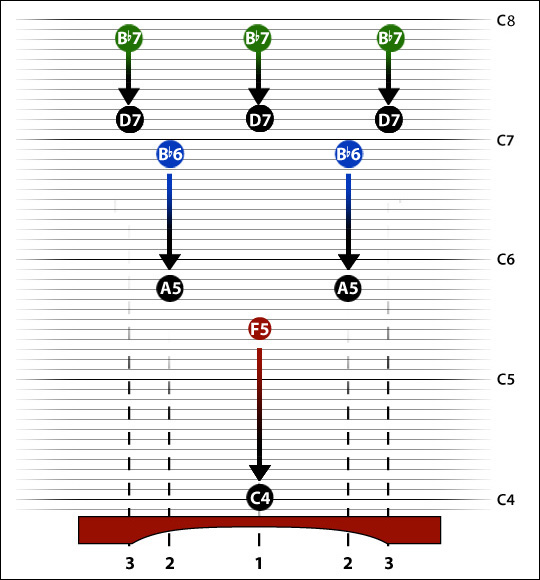
Can we carry our triple-tuning scheme up the keyboard? Suppose we cut a similar-shaped notch on a C4 bar. What happens? On our C3 bar we lowered the fundamental by 2 octaves (24 semitones or 2400 cents); the 2nd mode was lowered by approximately 17 semitones, and the third by 13 semitones. Proportions of 1 -- 0.73 -- 0.55. On the C4 bar remember, our initial pitch was F5; if we lower all the modes in the same proportions, the diagram comes out something like this:
We have overshot. If we want the bar to be tuned C4 -- C6 -- E7, we need to leave more material in place around the antinodes for modes 2 and 3. A curve like this will probably do it.
Yup....
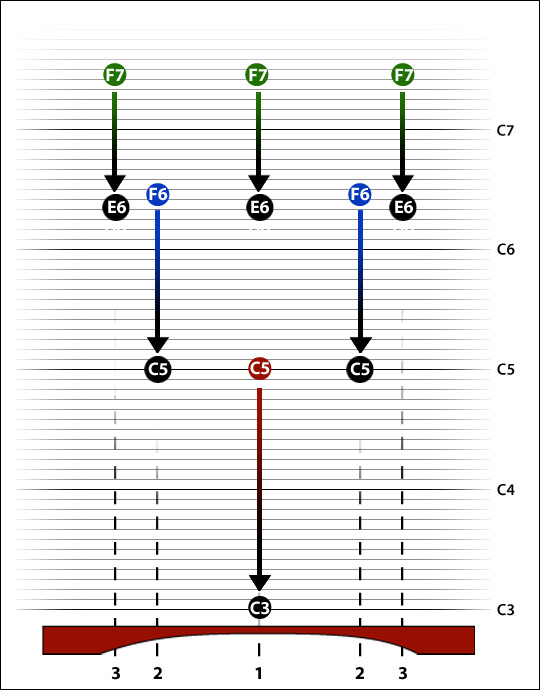
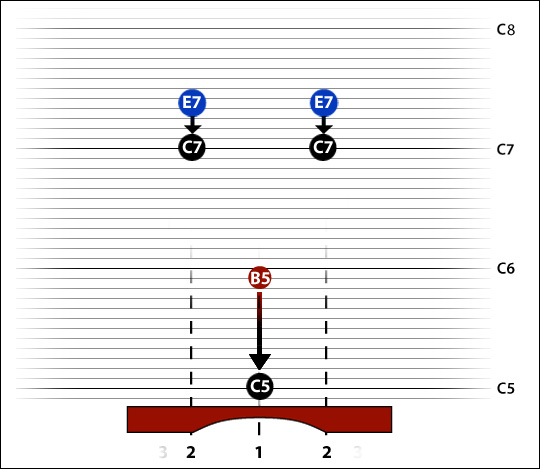
Lets move up to C5. At this pitch the third mode of vibration is going to be so high (and faint) that we'll be lucky to hear it at all, so let's forget about it for now. However tuning the 2nd mode is starting to be a bit problematic. Our initial pitch is B5, so the fundamental has to come down by 11 semitones; but the second mode only wants to come down by 4 and a half semitones. We'll need to cut a more truncated curve still, something like:--
to get:--
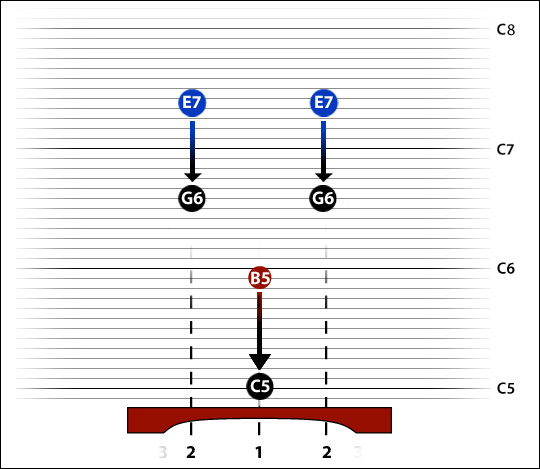
As you have probably worked out, on our C6 bar it is not possible to tune the second mode to the double octave, because it is already lower than we want on our blank (which has initial pitch F6; second mode technically B flat 7 +55).
So the double-octave tuning system, which seems so satisfactory and easy to produce for bars between C3 and C5, breaks down somewhere between C5 and C6.
But hold it! -- there is another available harmonic tone below that double octave. Our emerging theory of bar tuning suggests that reverting to a nice generous notch on the higher-pitched bars might bring our second mode into tune with the pitch one twelfth above the fundamental, so ... a bit more time on the beach and we produce this:
and its pitch-diagram ...
So all in all it's been a very useful day on the beach -- we have not only invented the modern marimba, but also the quint-tuned xylophone. Because if the double-octave tuning works sweetly over the (approximate) range C3 --> C5, the twelfth-tuning works just as nicely as well over the range C5 --> C7. A little finagling and you can quint-tune right down to C4.
Well, that's the theory -- the next post will be about the how and the who and the when.
****
Extra science credit! --
The simple formulae we discovered for bar size and pitch, i.e.
2L = f/4
and
t/2 = f/2
are outcomes of the real equation for the pitch of a free free bar, which can be expressed:
where --
f is frequency in Hz
a is thickness in metres
L is length in metres
Y is Young's modulus for the material the bar is made of, in gigapascals
d is density of the material, in kilograms per cubic metre
Is this useful information? Well, sure ... but if you have 49 marimba bars to tune by Wednesday afternoon?
NB All the basic physics/acoustics information in this post can be got from standard textbooks, probably going back to the 19th century. A convenient summary of the relevant info for instruments of all kinds can be found in Musical Instrument Design by Bart Hopkin ISBN 1-884365-08-6; check out his web site windworld